4 Parameter Estimation

The normal-exponential mixture has worked best under the availability of some relevance judgments which serve as an indication about the form of the component densities [8,3,22]. In filtering or classification, usually some training data--although often biased--are available. In the current task, however, no relevance information is available.

A method was introduced in the context of fusion which recovers the component densities without any relevance judgments using the Expectation Maximization (EM) algorithm [14]. In order to deal with the biased training data in filtering, the EM method was also later adapted and applied for thresholding tasks [1].⁴ Nevertheless, EM was found to be "messy" and sensitive to its initial parameter settings [1,14]. We will improve upon this estimation method in Section 4.3.

4.1 Down-truncated Rankings

For practical reasons, rankings are usually truncated at some rank $t < n$ . Even what is usually considered a full ranking is in fact a collection's subset of those documents with at least one matching term with the query.

This fact has been largely ignored in all previous research using the standard model, despite that it may affect greatly the estimation. For example, in TREC Legal 2007 and 2008, $t$ was $25,000$ and $100,000$ respectively. This results to a left-truncation of $P(s\vert 1)$ which at least in the case of the 2007 data is significant. For 2007 it was estimated that there were more than $25,000$ relevant documents for 13 of the 43 Ad Hoc topics (to a high of more than $77,000$ ) and the median system was still achieving $0.1$ precision at ranks of $20,000$ to $25,000$ .

Additionally, considering that the exponential may not be a good model for the whole distribution of the non-relevant scores but only for their high end, some imposed truncation may help achieve better fits. Consequently, all estimations should take place at the top of the ranking, and then get extrapolated to the whole collection. The truncated models of [5] require changes in the estimation formulas.

Let us assume that the truncation score is $s_t$ . For both truncated models, we we need to estimate a two-side truncated normal at $s_t$ and $s_{\max}$ , and a shifted exponential by $s_t$ right-truncated at $s_{\max}$ , with $s_{\max}$ possibly be $+\infty$ . Thus, the formulas that should be used are Equations 9 and 10 but for $\alpha_t$ instead of $\alpha$

$$\alpha_t = \frac{s_{t}-\mu} {\sigma}$$

and for $s_t$ instead of $s_{\min}$ . Beyond this, the models differentiate in the way $R$ is calculated.

If $G_t$ is the fraction of relevant documents in the truncated ranking, extrapolating the truncated normal outside its estimation range and appropriately per model in order to account for the remaining relevant documents, the $R$ is calculated as:

• theoretically truncated normal-exponential
  $$R = t\, G_t \, \frac{\Phi(\beta) - \Phi(\alpha)} {\Phi(\beta)-\Phi(\alpha_t)}$$

• technically truncated normal-exponential
  $$R = t\, G_t \, \frac{1} {\Phi(\beta)-\Phi(\alpha_t)}$$

Consequently, Equation 1 must be replaced by one of the above depending on the model in use, Equations 2 and 3 must be re-written as

$$R_+(s) = t \, G_t \, \left(1-F(s\vert 1)\right)$$

$$N_+(s) = t \, \left(1 - G_t \right) \left(1-F(s\vert)\right)$$

while Equations 4 and 5 remain the same. $F(s\vert 1)$ and $F(s\vert)$ are now the cdfs either of Section 3.3.1 or 3.3.2, depending on which model is used.

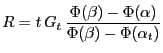
In estimating the technically truncated model, if there are any scores equal to $s_{\max}$ or $s_{\min}$ they should be removed from the data-set; these belong to the discontinuous legs of the densities given in Section 3.3.2. In this case, $t$ should be decremented accordingly. In practise, while scores equal to $s_{\min}$ should not exist in the top-$t$ due to the down-truncation, some $s_{\max}$ scores may very well be in the data. Removing these during estimation is a simplifing approximation with an insignificant impact when the relevant documents are many and the bulk of their score distribution is below $s_{\max}$ , as it is the case in current experimental setup. As we will see next, while we do not use the $s_{\max}$ scores during fitting, we take them into account during goodness-of-fit testing; using multiple such fitting/testing rounds, this reduces the impact of the approximation.

4.2 Score Preprocessing

Our scores have a resolution of $10^{-6}$ . Obviously, LUCENE rounds or truncates the output scores, destroying information. In order to smooth out the effect of rounding in the data, we add $\Delta s = \mathrm{rand}(10^{-6}) - 0.5*10^{-6}$ to each datum point, where $\mathrm{rand}(x)$ returns a uniformly-distributed real random number in $[0,x)$ .

Beyond using all scores available and in order to speed up the calculations, we also tried stratified down-sampling to keep only 1 out of 2, 3, or 10 scores.⁵Before any down-sampling, all datum points were smoothed by replacing them with their average value in a surrounding window of 2, 3, or 10 points, respectively.

In order to obtain better exponential fits we may further left-truncate the rankings at the mode of the observed distribution. We bin the scores (as described in Section A.1), find the bin with the most scores, and if that is not the leftmost bin then we remove all scores in previous bins.

4.3 Expectation Maximization

EM is an iterative procedure which converges locally [9]. Finding a global fit depends largely on the initial settings of the parameters.

4.3.1 Initialization

We tried numerous initial settings, but no setting seemed universal. While some settings helped a lot some fits, they had a negative impact on others. Without any indication of the form, location, and weighting of the component densities, the best fits overall were obtained for randomized initial values, preserving also the generality of the approach:⁶

$$G_{t,\mathrm{init}} = \mathrm{rand}(1) \,,\quad \lambda_\mathrm{init}= \max(\epsilon, \mathrm{rand}(\mu_s -s_t))^{-1}$$

$$\mu_\mathrm{init}= s_{\min} + \mathrm{rand}( s_1-s_{\min} )$$

$$\sigma^2_\mathrm{init}= \max( \epsilon^2, (1+ c_1\mathrm{rand}(1))^2 \sigma_s^2 - \lambda_\mathrm{init}^{-2} )$$

where $s_1$ is the maximum score datum, $\mu_s$ and $\sigma_s^2$ are respectively the mean and variance of the score data, $\epsilon$ is an arbitrary small constant which we set equal to the width of the bins (see Appendix A.1), and $c_1 \in (0,+\infty)$ is another constant which we explain below.

Assuming that no information is available about the expected $R$ , not much can be done for $G_{t,\mathrm{init}}$ , so it is randomized using its whole supported range. Next we assume that right-truncation of the exponential is insignificant, which seems to be the case in our current experimental set-up.

If there are no relevant documents, then $\mu_s - (s_t-s_{\min}) \approx \lambda^{-1}+s_{\min}$ . From the last equation we deduce the minimum $\lambda_\mathrm{init}$ . Although in general, there is no reason why the exponential cannot fall slower that this, from an IR perspective it should not, or $\mathrm{E}(S_{\mathrm{nrel}})$ would get higher than $\mathrm{E}(S_{\mathrm{rel}})$ .

The $\mu_\mathrm{init}$ given is suitable for a full normal, and its range should be expanded in both sides for a truncated one because the mean of the corresponding full normal can be below $s_{\min}$ or above $s_1$ . Further, $\mu_\mathrm{init}$ can be restricted based on the hypothesis that for good systems should hold that $\mathrm{E}(S_{\mathrm{rel}}) > \mathrm{E}(S_{\mathrm{nrel}})$ . We have not worked out these improvements.

The variance of the initial exponential is $\lambda_\mathrm{init}^{-2}$ . Assuming that the random variables corresponding to the normal and exponential are uncorrelated, the variance of the normal is $\ge \sigma_s^2 - \lambda_\mathrm{init}^{-2}$ which, depending on how $\lambda$ is initialized, could take values $\le 0$ . To avoid this, we take the max with the constant. For an insignificantly truncated normal, $c_1 \approx 0$ , while in general $c_1 >0$ , because the variance of the corresponding full normal is larger than what is observed in the truncated data. We set $c_1=2$ , however, we found its usable range to be $[0.25,5]$ .

4.3.2 Update Equations

For $t \le n$ observed scores $s_1\ldots s_t$ , and neither truncated nor shifted normal and exponential densities (i.e. for the original model), the update equations are

$$G_{t,\mathrm{new}} = \frac{\sum_i P_{\mathrm{old}}(1\vert s_i)}{t... ...\frac{\sum_i P_\mathrm{old}(0\vert s_i)}{\sum_i P_\mathrm{old}(0\vert s_i) s_i}$$

$$\mu_\mathrm{new}= \frac{\sum_i P_\mathrm{old}(1\vert s_i) s_i}{\s... ...old}(1\vert s_i) (s_i - \mu_\mathrm{new})^2}{\sum_i P_\mathrm{old}(1\vert s_i)}$$

$P(j\vert s)$ is given by Bayes' rule $P(j\vert s) = {P(s\vert j) P(j)}/{P(s)}$ , $P(1) = G_t$ , $P(0) = 1-G_t$ , and $P(s)$ by Equation 3.1.

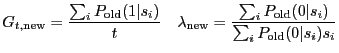
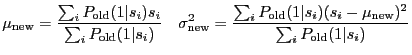
We initialize those equations as described above, and iterate them until the absolute differences between the old and new values for $\mu$ , $\lambda^{-1}$ , and $\sqrt{\sigma}$ are all less than $.001\, (s_1 - s_{\min})$ , and $\vert G_{t,\mathrm{new}} - G_{t,\mathrm{old}} \vert < .001$ . Like this we target an accuracy of 0.1% for scores and 1 in a 1,000 for documents. We also tried a target accuracy of 0.5% and 5 in 1,000, but it did not seem sufficient.

4.3.3 Correcting for Truncation

If we use the truncated densities (Equations 9 and 10) in the above update equations, the $\mu_\mathrm{new}$ and $\sigma_\mathrm{new}^2$ calculated at each iteration would be the expected value and variance of the truncated normal, not the $\mu$ and $\sigma^2$ we are looking for. Similarly, $1/\lambda_\mathrm{new}+ s_t$ would be equal to the expected value of the shifted truncated exponential. Instead of looking for new EM equations, we rather correct to the right values using simple approximations.

Using Equation 26, at the end of each iteration we correct the calculated $\lambda_\mathrm{new}$ as

$$\lambda_\mathrm{new}\leftarrow \left( \frac{1}{\lambda_\mathrm{ne... ...}-s_{t})) - s_{t} } { \Psi(s_{\max} -s_{t};\lambda_\mathrm{old}) } \right)^{-1}$$ (12)

using the $\lambda_\mathrm{old}$ from the previous iteration as an approximation. Similarly, based on Equations 24 and 25, we correct the calculated $\mu_\mathrm{new}$ and $\sigma_\mathrm{new}^2$ as

$$\mu_\mathrm{new}\leftarrow \mu_\mathrm{new} - \frac{\phi(\alpha') - \phi(\beta') } {\Phi( \beta' ) - \Phi( \alpha') } \sigma_\mathrm{old}$$ (13)

$$\sigma_\mathrm{new}^2 \leftarrow \sigma_\mathrm{new}^2 \left[ 1 +... ...(\alpha') - \phi(\beta')} {\Phi(\beta') - \Phi(\alpha')} \right)^2 \right]^{-1}$$ (14)

where

$$\alpha' = \frac{s_t-\mu_\mathrm{old}} {\sqrt{\sigma_\mathrm{old}^... ...\quad \beta' = \frac{s_{\max}-\mu_\mathrm{old}} {\sqrt{\sigma_\mathrm{old}^2}}$$

again using the values from the previous iteration.

These simple approximations work, but sometimes they seem to increase the number of iterations needed for convergence, depending on the accuracy targeted. Rarely, and for high accuracies only, the approximations possibly handicap EM convergence; the intended accuracy is not reached for up to 1,000 iterations. Generally, convergence happens in 10 to 50 iterations depending on the number of scores (more data, slower convergence), and even with the approximation EM produces considerably better fits than when using the non-truncated densities. To avoid getting locked in a non-converging loop, despite its rarity, we cap the number of iterations to 100. The end-differences we have seen between the observed and expected numbers of documents due to these approximations have always been less than 4 in 100,000.

4.3.4 Multiple Runs

We initialize and run EM as described above. After EM stops, we apply the $\chi^2$ goodness-of-fit test for the observed data and the recovered mixture (see Appendix A). If the null hypothesis $\mathrm{H}_0$ is rejected, we randomize again the initial values and repeat EM for up to 100 times or until $\mathrm{H}_0$ cannot be rejected. If $\mathrm{H}_0$ is rejected in all 100 runs, we just keep the best fit found. We run EM at least 10 times, even if we cannot reject $\mathrm{H}_0$ earlier. Perhaps a maximum of 100 EM runs is an overkill, but we found that there is significant sensitivity to initial conditions.

4.3.5 Rejecting Fits on IR Grounds

Some fits, irrespective of their quality, can be rejected on IR grounds. Firstly, it should hold that $R \le n$ , however, since each fit corresponds to $t\,\left(1-G_t\right)$ non-relevant documents, we can tighten the inequality somewhat to:

$$R \le n - t\,\left(1-G_t\right)$$ (15)

This is a very light condition, which should handle a few extremities.

Table: The effects of sampling and binning on fitting quality, and convexity of fits.

run	$\widetilde{M}$	$M > 190$	$\mathrm{H}_0$ no reject	$k_c>1$	$\widetilde{k_c}$	$k_c > \widetilde{R}$	comments
2007-default	56.5	4 (8%)	2 (4%)	33 (66%)	29	5 (10%)	no smth or sampling
2007-A	37	1 (2%)	32 (64%)	40 (80%)	34	5 (10%)	smth + 1/3 strat. sampl.
2007-B	36	1 (2%)	30 (60%)	32 (64%)	61.5	1 (2%)	smth + 1/3 strat. sampl.
2008-default	93	6 (13%)	0 (0%)	29 (64%)	89	0 (0%)	no smth or sampling
2008-A	63	1 (2%)	5 (11%)	30 (67%)	98	0 (0%)	smth + 1/3 strat. sampl.
2008-B	66	4 (9%)	9 (20%)	31 (69%)	45	1 (2%)	smth +1/3 strat. sampl.

Secondly, concerning the random variables $S_\mathrm{rel}$ and $S_\mathrm{nrel}$ , one would expect:

$$\mathrm{E}(S_\mathrm{rel}) > \mathrm{E}(S_\mathrm{nrel})$$ (16)

This is rather only a hypothesis--not a requirement--that good systems should satisfy and there are no guarantees. We have not been able so far to motivate any inequality on score variances.

We are still experimenting with such conditions, and we have not applied them for producing any of the end-results reported in this paper.

4.4 Fitting Results and Analysis

While the s-d method is non-parametric, there are several parameters in recovering the mixture of the densities: smoothing and sampling (both optional), binning, EM initialization and targeted accuracy, rejection conditions, and maybe others. Table 1 provides some data on the fits resulting from the above procedure. The default and A runs use the theoretical truncation of Section 3.3.1; the B runs use the technical truncation of Section 3.3.2.

4.4.1 Sampling, Binning, and Quality of the Fits

Down-sampling has the effect of eliminating some of the right tails, leading to fewer bins when binning the data. Moreover, the fewer the scores, the less EM iterations and runs are needed for a good fit (data not shown). Down-sampling the scores helps supporting the $\mathrm{H}_0$ . At 1 out of 3 stratified sampling, the $\mathrm{H}_0$ cannot be rejected at a significance level of 0.05 for 60-64% of the 2007 topics and for 20% for the 2008 topics. Non-stratified down-sampling with 0.1 probability raises this to 42% for the 2008 topics. Extreme down-sampling to keep only around 1,000 to 5,000 scores supports the $\mathrm{H}_0$ in almost all fits.

Consequently, the number of scores and bins plays a big role in the quality of the fits according to the $\chi^2$ test; there is a positive correlation between the median number of bins $\widetilde{M}$ and the percentage of rejected $\mathrm{H}_0$ . This effect does not seem to be the result of information loss due to down-sampling; we still get more support for the $\mathrm{H}_0$ when reducing the number of scores by down-truncating the rankings instead of down-sampling them. This is an unexpected result; we rather expected that the increased number of scores and bins is dealt with by the increased degrees of freedom parameter of the corresponding $\chi^2$ distributions. Irrespective of sampling and binning, however, all fits look reasonably well to the eye.

4.4.2 A Score Continuity Problem?

In all runs, for a small fraction of topics (2-13%) the optimum number of bins $M$ is near ($<5\%$ difference) to our capped value of 200. For most of these topics, when looking for the optimal number of bins in the range $[5, 1000]$ (numbers are tried with a step of 5%) the binning method does not converge. This means there is no optimal binning as the algorithm identifies the discrete structure of data as being a more salient feature than the overall shape of the density function. Figure 4 demonstrates this.

Figure: The optimal number of bins does not seem to converge, so it is capped at 200. Due to the high number of bins, the best fit found has a large $\chi^2 = 2231.4$ . Combining bins with expected frequency $<5$ on the right tail, minus 4 the parameters we estimate, gives 84 degrees of freedom for the $\chi^2$ distribution and a critical value of $106.4$ at .05 significance. The upper-probability of the fit is practically 0, nevertheless, it looks reasonably well to the eye.

Since the scores are already randomized to account for rounding (Section 4.2), the discrete structure of the data is not a result of rounding but it rather comes from the retrieval model itself. Internal statistics are usually based on document and word counts; when these are low, statistics are "rough", introducing the discretization effect.

4.4.3 Convexity of Fits

Concerning the theoretical anomaly of the normal-exponential mixture, we investigate the number of fits presenting the anomaly within the observed score range, i.e. at a rank below rank-1 ($k_c >1$ ).⁷ We see that the anomaly shows up in a large number of topics (64-80%). The impact of non-convexity on the s-d method is that the method turns "blind" at rank numbers $<k_c$ restricting the estimated optimal thresholds wtih $K \ge k_c$ . However, the median rank number $\widetilde{k_c}$ down to which the problem exists is very low compared to the median estimated number of relevant documents $\widetilde{R}$ (7,484 or 32,233), so $K < k_c$ is unlikely on average anyway and thresholding should not be affected. Consequently, the data suggest that the non-convexity should have an insignificant impact on s-d thresholding.

For a small number of topics (0-10%), the problem appears for $k_c > \widetilde{R}$ and non-convexity should have a significant impact. Still, we argue that for a good fraction of such topics, a large $k_c$ indicates a fitting problem rather than a theoretical one. Figure 5 explains this further.

Figure: For topic 91 (top plot), the fit looks good but has a convexity problem in the whole ranking ( $k_c \ge 25,000$ ), indicated by having to flatten its precision in the whole range. Alternatively, the fit could have been rejected on IR grounds. By enabling the condition of Equation 16, i.e. the expected relevant score should be larger than the expected non-relevant, the method would have rejected the fit and produce another one (bottom plot) with a slightly larger $\chi^2$ but no convexity problem. (Both datasets are downsampled; the slight variation of the observed data across the plots are due to different samples used.)

4.4.4 Ranking-length Bias

Since there are more data at lower scores, EM results in parameter estimates that fit the low scores better than the high scores. This is exactly the opposite of what is needed for IR purposes, where the top of rankings is more important. It also introduces a weak but undesirable bias: the longer the input ranked list, the lower the estimates of the means of the normal and exponential; this usually results in larger estimations of $R$ and $K$ .

Trying to neutralize the bias without actually removing it, input ranking lengths can better be chosen according to the expected $R$ . This also makes sense for the estimation method irrespective of biases: we should not expect much when trying to estimate, e.g., an $R$ of 100,000 from only the top-1000. As a rule-of-thumb, we recommend input ranking lengths of around 1.5 times the expected $R$ with a minimum of 200. According to this recommendation, the 2007 rankings truncated at 25,000 are spot on, but the 100,000 rankings of 2008 are falling short by 20%.

4.5 Summary and Future Improvements

Recovering the mixture with EM has been proven to be "tricky". However, with the improvements presented in this paper, we have reached a rather stable behavior which produces usable fits.

EM's initial parameter settings can further be tightened resulting in better estimates in less iterations and runs, but we have rather been conservative in order to preserve the generality.

As a result of how EM works--giving all data equal importance--a weak but undesirable ranking-length bias is present: the longer the input ranking, the larger the $R$ estimates. Although the problem can for now be neutralized by choosing the input lengths in accordance with the expected $R$ , any future improvements of the estimation method should take into account that score data are of unequal importance: data should be fitted better at their high end.

Whatever the estimation method, conditions for rejecting fits on IR grounds such as those investigated in Section 4.3.5, seem to have a potential for further considerable improvements.

Footnotes

...ArampatzisTREC:01.⁴

Another method for producing unbiased estimators in filtering can be found in [22], but it requires relevance judgements.

... scores.⁵

In order not to complicate things further, we do not include the down-sampling into the formulas in this paper; it is not difficult to see where things should be weighted inversely proportional to the sampling probability.

... approach:⁶

With some (even biased) training data, suitable initial parameter settings are given in [1]. Without any training data, assuming that the relevant documents are much fewer than non-relevant by rank $t$ , initial parameters can be estimated as described in [14]; unfortunately this assumption cannot be made in TREC Legal due to the large variance of estimated $R$ and topics with $R > t$ .

...).⁷

In our context we re-formulated the recall-fallout convexity hypothesis as a condition on smoothed precision. So there is no issue of convexity but rather the issue of the precision monotonically declining with the score. However, we stick to using the term "convexity" in describing the problem.